IOI2020 Day2 stations 풀이

문제 및 채점: oj.uz

 

$N$ 개의 정점으로 이루어진 트리가 주어진다. 각 정점에 $0$ 이상 $K$ 이하의 수를 서로 다르게 적는다. 수 $i$가 적힌 정점을 정점 $i$라고 하자. 정점 $s$에 인접한 정점에 적힌 수들이 배열 $c$로 주어질 때, 정점 $s$에서 정점 $t$로 가기 위해 어느 인접한 정점으로 이동하면 되는지 구하는 질문이 주어진다. 문제는 정점에 수를 적는 함수와, 주어지는 질문을 해결하는 함수 두 개를 작성하는 것이다. 단, 정점에 적는 수 이외에 전역 변수와 같이 외부 메모리를 참조하여 질문을 해결할 수 없다.

 

서브태스크 1, 2, 3, 4

이 서브태스크에 대한 풀이는 따로 서술하지 않겠다. 서브태스크 1, 2, 3은 주어지는 트리의 모양이 일자, 완전 이진 트리 등 정해진 모양을 가지며, 그 모양에 따라 수를 적절히 적어주어 주어지는 질문을 해결할 수 있다.

 

서브태스크 5

임의의 정점을 루트로 정해 루트가 있는 트리로 만든다. 루트부터 시작하여 dfs 순서로 정점을 탐색하며 1부터 $N$까지의 수를 적는데 정점 깊이의 홀짝성에 따라 수를 preorder, postorder로 적는다.

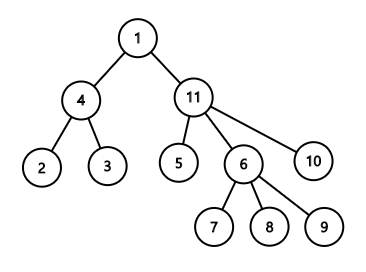
위 그림은 트리에서 언급한 방식으로 정점에 수를 적은 예시이다. 정점 11에서 시작하여, 10 이상 11 미만의 번호가 적힌 정점으로 가기 위해서는 정점 10으로 가야 하고, 6 이상 10 미만의 번호가 적힌 정점으로 가기 위해서는 정점 6으로 가야 하고, 5 이상 6 미만의 번호가 적힌 정점으로 가기 위해서는 정점 5로 가야 하고, 1이상 5 미만의 번호가 적힌 정점으로 가기 위해서는 정점 1로 가야 한다. 정점 1에서 시작하여, 1 초과 4 이하의 번호가 적힌 정점으로 가기 위해서는 정점 4로 가야 하고, 4 초과 11 미만의 번호가 적힌 정점으로 가기 위해서는 정점 11로 가야 한다. 이와 같이 정점에 번호를 적을 경우, 가려고 하는 정점에 적힌 번호와 인접한 정점에 적힌 번호를 기반으로 간단하게 주어지는 질문을 해결할 수 있다.

 

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

#include <bits/stdc++.h> #include "stations.h" using namespace std;   vector<int> label(int N, int K, vector<int> u, vector<int> v) {     vector<vector<int>> con(N);     for (int i=0;i<N-1;i++)         con[u[i]].push_back(v[i]),         con[v[i]].push_back(u[i]);       vector<int> labels(N); int idx = 0;     function<void(int, int)> dfs;     dfs = [&](int n, int p){         if (p == -1 || !labels[p]) labels[n] = ++idx;         for (int t: con[n]) if (t != p)             dfs(t, n);         if (!labels[n]) labels[n] = ++idx;     };     dfs(0, -1);     return labels; }   int find_next_station(int s, int t, vector<int> c) {     if (c.back() < s) reverse(c.begin(), c.end());     for (int x: c) if (min(s, x) <= t && t <= max(s, x)) return x;     return c.back(); }